§3.7 曲线的凹凸与拐点

一、引例

研究了函数的单调性、极性，对于函数的性态有了更进一步的了解。为了描绘出函数的图象的主要特征，仅凭此两点还是不够的。

【引例】作函数与在 上的图象。

曲线的凹凸的特性可由下面的几何图形所反映出的事实看出：

二、凹凸的定义

设函数在上连续， 如果对上任意、两点， 恒有

则称曲线在上的是凹的(或凹弧)，也称函数是上的凹函数。

如果恒有

则称曲线在上是凸的(或凸弧)，也称函数是上的凸函数。

函数的一阶导数的符号可判断函数的单调性，二阶导数的符号又能确定函数的何种属性呢?一个最简单的例子，给我们以启迪。

抛物线的二阶导数为，

若， 即，抛物线是开口向上的凹弧；

若， 即，抛物线是开口向下的凸弧。

三、凹凸性的判别法

【定理】

设函数在上连续， 在内具有一阶和二阶导数，那未

(1)、若在内， ，则在上的图形是凹的；

(2)、若在内， ，则在上的图形是凸的。

证明(仅证(2))：

， 且 ， 记 ，

，

由拉氏中值公式有

两式相减得：

对在区间上再一次地使用拉氏中值公式有：

其中： 。

依定理情形(2)的假设条件有， 从而

，即

，亦即

所以， 函数在上是凸的。

对此定理，我们给出两点注释。

1、定理的记忆方法

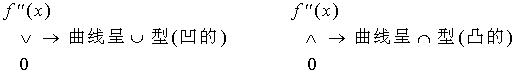
2、函数在任意区间上凹凸性的定义与判定与之相类似。

四、曲线的拐点

业已知道，函数一阶导数为零或不存在的点，是函数单调区间的分界点，且函数在它左右两侧的单调性往往是相反的。

能否猜想：函数二阶导数为零或不存在的点，它所对应的曲线上的点是曲线弧的凹弧与凸弧的分界点。

【拐点定义】连续曲线上的凹弧与凸弧的分界点称为该曲线的拐点。

依拐点的定义， 不难给出确定曲线拐点的方法：

设函数在区间上连续

1、求出在上为零或不存在的点；

2、这些点将区间划分成若干个部分区间，然后考察在每个部分区间上的符号，确定曲线的凹凸性；

3、若在两个相邻的部分区间上，曲线的凹凸性相反，则此分界点是拐点；若在两个相邻的部分区间上，曲线的凹凸性相同，则此分界点不是拐点。

【例1】求曲线的凹凸区间与拐点。

解：函数的定义区间为 ，，

，令 得：。

将定义区间分为三个区间

当时，，点是曲线的一个拐点；

当时，，点也是曲线的一个拐点。

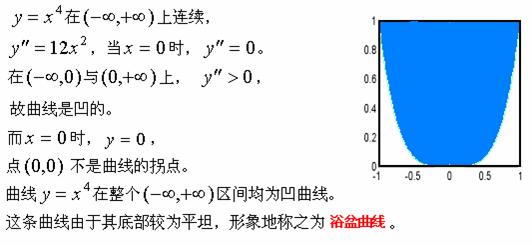
【例2】讨论曲线的凹凸性与拐点。